In 2016, Magic Leap released Deep Image Homography Estimation, in which a homography is estimated with a neural network instead of the traditional geometric approach. No code was released, so I was curious to play around with it. My code can be found on GitHub.

A homography defines a transformation between two planes, including:

  • An image plane and a planar object.
  • Two different views of a planar object (or a very distant scene).
  • Two images taken by a rotating camera.

Homographies are used in panorama stitching, camera calibration, and estimation of the camera pose.

As a 2D perspective transform in homogeneous coordinates, a homography can be represented as a 3x3 matrix, with 8 degrees of freedom. Estimating the homography requires 4 matching points in each image. If exact correspondences are not known, more points are provided and a technique like RANSAC is used.

The authors of this paper do not learn the 8 parameters of the homography matrix directly, as it is notorously difficult to learn a target consisting of rotational and translational terms. The target is instead the x and y perturbations (in pixels) to the 4 corners of the patch extracted in estimating the homography.

dataset generation procedure

The main contribution from the authors is a means to generate an endless supply of homography data. MS-COCO images are resized to 320x240, converted to grayscale, then a 128 pixel patch is extracted. The x and y coordinates of each patch corner are perturbed by a random amount between -32 and 32. With the 4 corresponding corners, the transform from the perturbed corners to the original can be estimated. The transform is applied to the image and then a 128x128 patch, at the same location as the original image, is extracted. The result is a pair of images that can be stacked in the channel dimension and a set 8 values, which define a homography. This serves as the input and target data for a neural network.

Notes

  • The authors took the inverse of the homography between the original and perturbed corners, when they could have just estimated the homography between the perturbed and original.
  • This dataset is created to simulate two different views of the same object. It would not work for homographies defining rotational views, as in panorama stitching, since there would be very little overlap in the patches.
  • The authors did not mention scaling the corner perturbations, but I found dividing by 32 and putting a tanh layer on the output of the network was necessary for training.

Results

I implemented the regression form of their network, and followed the dataset prep, architecture, and training parameters specified in the paper.

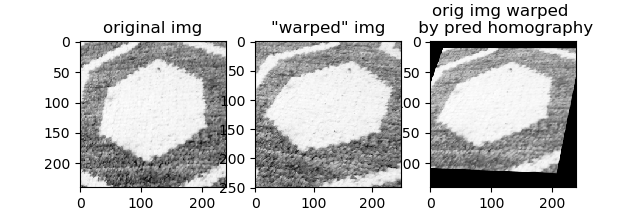
The network is very accurate on the synthetic data. Below are the original and warped patch, which are fed to the network as a 128x128x2 image. The predicted homography for this pair is applied to the original image to produce the image in the third column.

The image warped by the predicted homography is very similar to the image warped by the true homography.

good performance on test image

good performance on test image

Transfer to real data

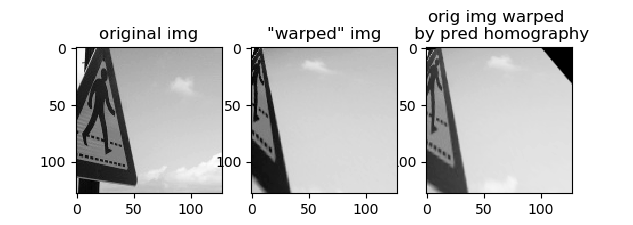
The problem with the data generation is that it treats every object in the image as being coplanar. This produces some unnatural images:

bad performance on test image

This makes me doubt that this network will work for any real data, outside of very special circumstances. For example, running the network on two views of a crosswalk sign from Google Maps yields:

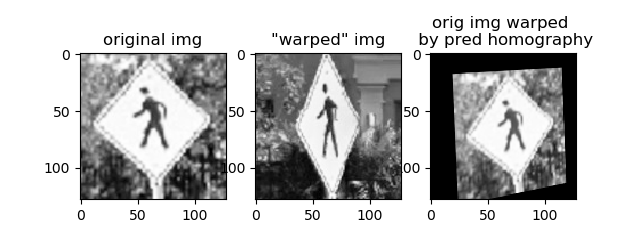
real image from Google Maps

The network is unsuccessful for this image pair consisting of objects on multiple planes. While there are plenty of signs in the training dataset, the background does not undergo the same transformation between the two images as the sign.

The network does better for a pair of images on the same plane, such as these two images of my rug:

real image of carpet